Precision and Quantization
Mind your P's and Q's
Word from the street- the recent uptick in popularity of small open-source models have upstaged “Pleases" and "thank-you’s" with their successor - Precision and Quantization.
This newsletter grows entirely due to you, dear reader. So, if you found this newsletter useful - subscribe, share it with your friends.
Tricks based on Precision and Quantization of LLMs shares it’s motivations with the previous post on PEFT, which comes down to optimizing the memory and compute required to run LLMs with lower resources. And given that lowering precision and quantizing models is growing in adoption, here are some notes briefly explaining them.
Precision
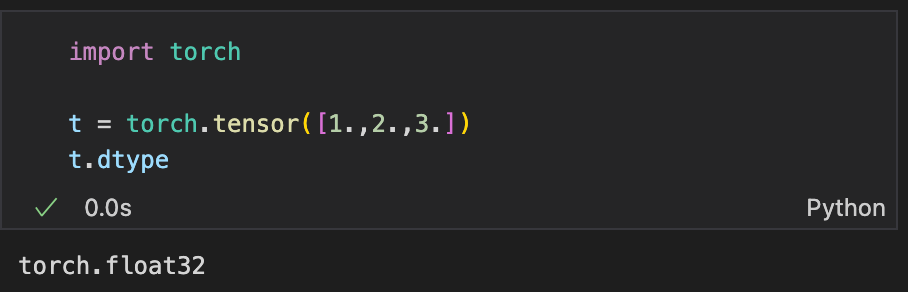
Underneath all the jargon and , LLMs are neural networks. And neural networks are sequences of matrices containing weights, which are typically stored as tensors. These tensors are, by default, stored in floating point-32 (float32) format, as you might have observed while creating tensors with pytorch.
Let’s go one level deeper. What does float32 mean?
Going back to the basics of computer science, floating point numbers are internally stored using bits of 0s and 1s reserving for sign, exponent and fraction/mantissa. So a 32 bit floating point representation of a number can be illustrated as follows - 1 bit for the sign, 8 bits for exponent and 23 bits for the fraction/decimals:

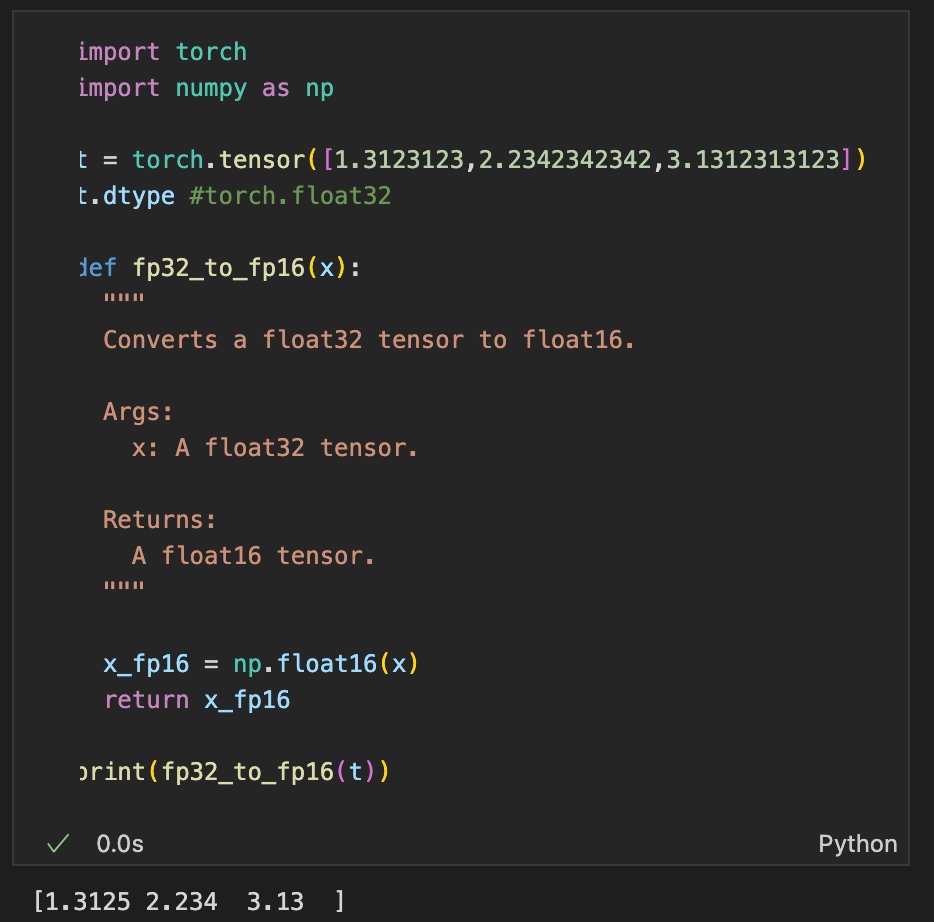
Precision can be lowered using other datatypes like half-precision (float16) which uses only 16 bits and thus requires half the memory. This lowers the memory required to store these numbers.
In python, this conversion can be achieved as follows:
Of-course, there is an accuracy tradeoff with lowering precision, which can lead to accumulation of rounding errors. However, literature shows using half-precision for model training has shown to work reasonably well. On a slight tangent, mixed precision means using different data types in different parts of the network so as to strike a balance between precision and memory management.
Really, how much memory is needed to run an LLM?
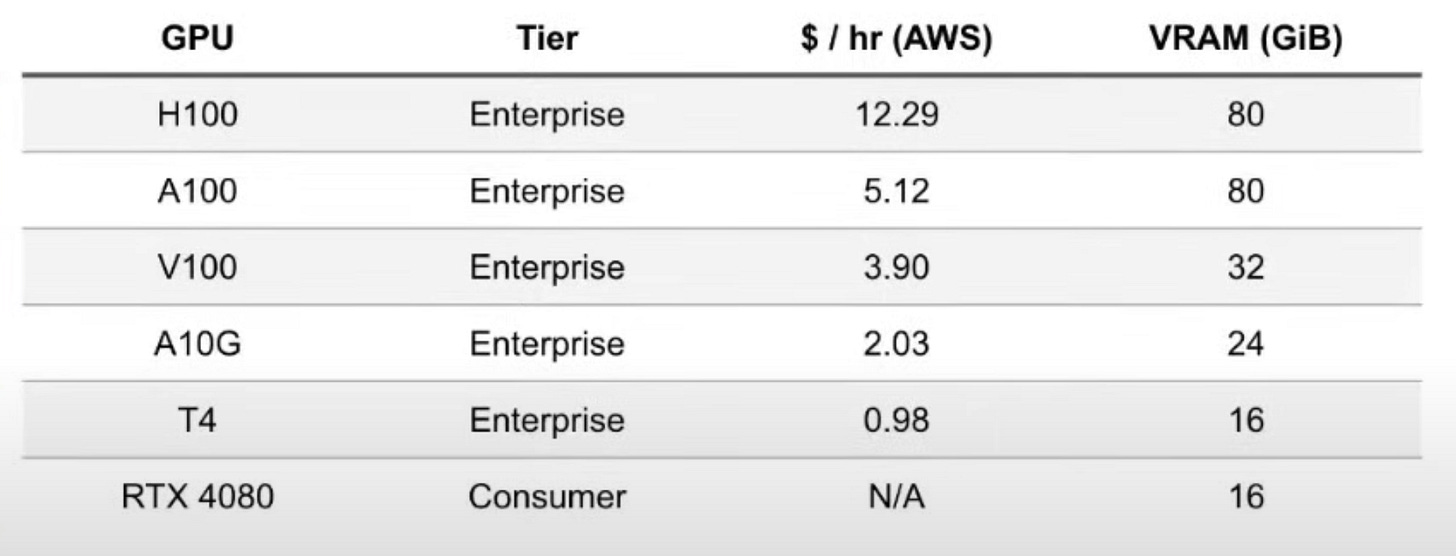
This leads us to the Memory Bottleneck. The following table shows the VRAM (memory) available in the latest GPUs. Among these, the most widely accessible by far is what is provisioned on Google Colab, which is the 16GB T4 GPU.
So the next question is how much memory is needed to load the modest Llama2-7b model. It is quite straightforward to estimate model size as shown below.
Model size = #bits in each weight x no of weights
Given the 7 billion parameters in llama2-7b, this amounts to:
7b x 32 bits per parameter / (8 bits per byte) = 28 GB
Already, we are beyond the capacity of the bottom 3 GPUs in the table. In addition to loading the model, training the model requires even more memory as we need to store the gradients (same as no of params; so another 28GB) and optimizer state to track each parameter (twice the no of params for the SOTA Adam optimizer to save the momentum and variance vectors; so 56 GB).
In total, this adds up to 112 GB. Ok, 32-bit representation is not an option.
Using half-precision (16-bit) does lower the model load memory to 14GB, however, we quickly run out of memory for training the model.
So… can we go lower than 16-bit without creating new issues? Maybe 8-bit?
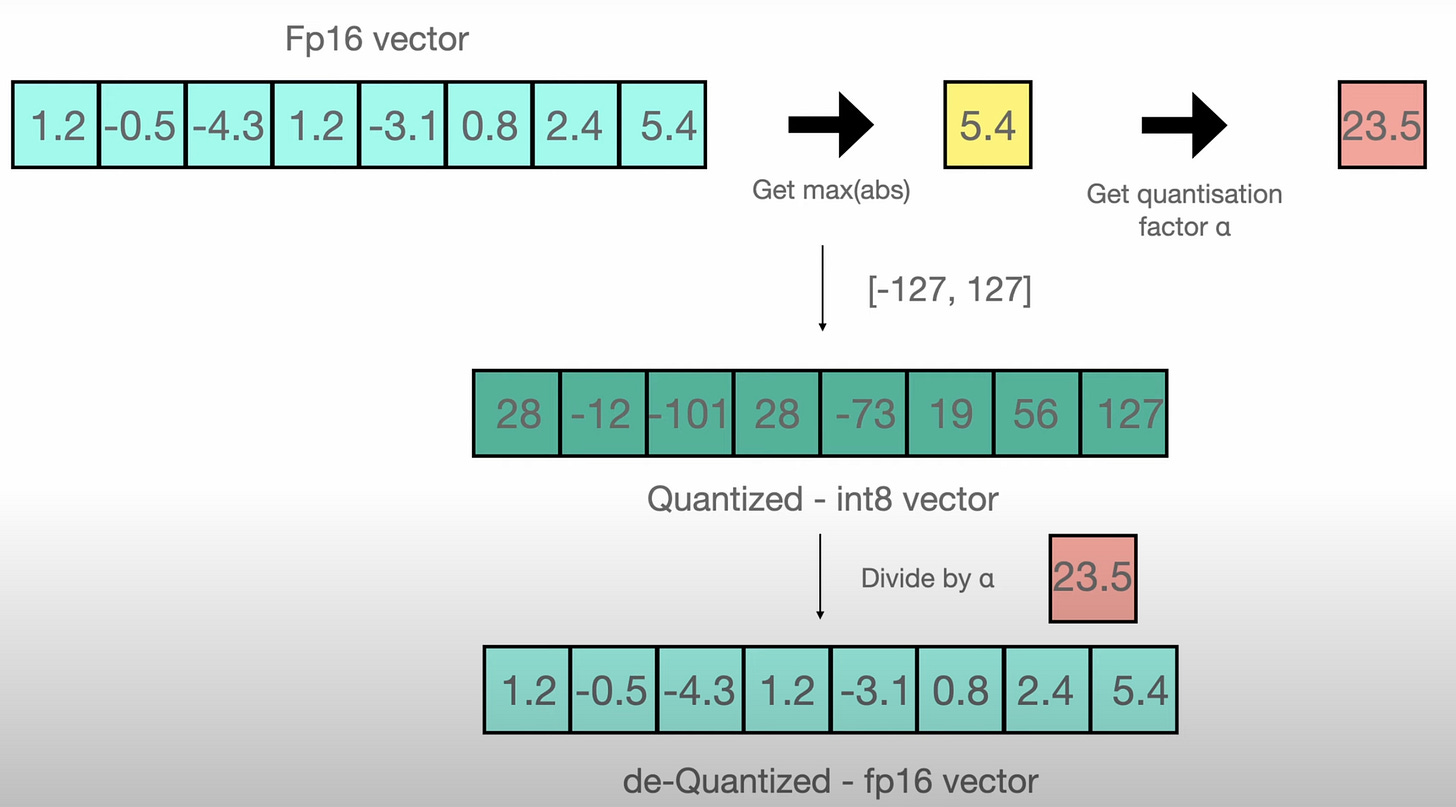
Quantization
This is what Quantization enables by not simply dropping precision (which can lead to other issues like exploding and vanishing gradients) but instead by calculating a quantization factor to scale the weights to lower precision (even integers). In essence, quantization has the effect of discretizing a ‘continuous’ space (32-bit) into bins with greater resolution (smaller bins) in the dense region of the distribution, and lower resolution at the tails.
This is improvement reducing the model and gradients down to 7GB each, however, the optimizer states would still require 56 GB.
So clearly, the Ps and Qs are not sufficient by itself, at least for the lay Google-Colab- T4 user to run modest 7b size models. In the next post, we shall see how LoRA solves this :)